Introduction
The world is an uncertain place. How to measure and deal with uncertain quantities is an important problem for basically all branches of science, in particular, for measure theory, statistics, data science and finance.
The typical mathematical structure that is used nowadays is a probability space ![]() . Thereby, the sample space
. Thereby, the sample space ![]() is a given non-empty set and
is a given non-empty set and ![]() the (linear) expected value of a random variable
the (linear) expected value of a random variable ![]() with respect to the probability measure
with respect to the probability measure ![]() .
.
This mathematical model, however, requires strong assumptions that are quite often not fulfilled in real world. It is rare to find situations in which a probability measure ![]() fully reflects the corresponding real world situation. In finance, for instance, the normal distribution assumption is heavily used even though it is often not fulfilled.
fully reflects the corresponding real world situation. In finance, for instance, the normal distribution assumption is heavily used even though it is often not fulfilled.
Data can be scarce and human behavior might also be involved. In these cases, the uncertainty of the probability itself becomes a hard problem and using probability measures might not be sufficient anymore, for instance, due to the Ellsberg Paradox. In the theory of economics, this type of higher level uncertainty is known as Knightian uncertainty.
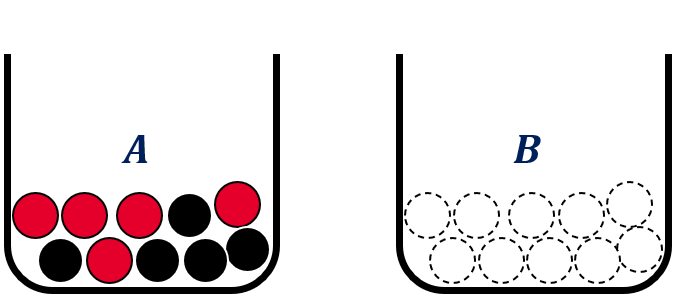
Example 1.1 (Ellsberg Paradox):
A person is shown two urns, ![]() and
and ![]() . Each of them containing 10 balls of red or black color. Urn
. Each of them containing 10 balls of red or black color. Urn ![]() contains 5 black and 5 red balls while there is no additional information about urn
contains 5 black and 5 red balls while there is no additional information about urn ![]() . That is, all balls in urn
. That is, all balls in urn ![]() could be black or red or any combination in between.
could be black or red or any combination in between.
 and
and  each containing 10 balls whereby we do not know the distribution of the color red and black in urn
each containing 10 balls whereby we do not know the distribution of the color red and black in urn 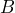
One ball is drawn at random from each urn. The person is offered to make a bet on color of the ball chosen from either urn. Winning a bet the person receives, say, 1000 €. Possible bets are, for example, ‘the ball drawn from urn A is black’ denoted by ![]() , ‘the ball drawn from urn
, ‘the ball drawn from urn ![]() is red’ denoted by
is red’ denoted by ![]() , and, similarly
, and, similarly ![]() and
and ![]() . Let us assume that the person can pick one option for each of the following four bets:
. Let us assume that the person can pick one option for each of the following four bets:
- Bet on
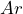 ,
, 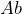 or indifferent;
or indifferent; - Bet on
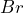 ,
, 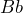 or indifferent;
or indifferent; - Bet on
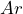 ,
, 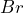 or indifferent;
or indifferent; - Bet on
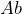 ,
, 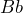 or indifferent;
or indifferent;
We denote the corresponding probabilities of an occurrence of ![]() and
and ![]() by
by ![]() and
and ![]() , respectively. A similar notation is used for the occurrence of
, respectively. A similar notation is used for the occurrence of ![]() and
and ![]() . The probabilities of
. The probabilities of ![]() and
and ![]() as well as
as well as ![]() and
and ![]() both each add up to
both each add up to ![]() given the additivity of the model.
given the additivity of the model.
It has been observed empirically that most subjects prefer any bet on urn A to a bet on urn ![]() The decision that most subjects make with respect to the four bets is usually indifferent for 1. and 2.,
The decision that most subjects make with respect to the four bets is usually indifferent for 1. and 2., ![]() for 3. and
for 3. and ![]() for 4..
for 4..
From the empirically suggested choice for bet 3. of drawing a red ball in urn ![]() , we infer
, we infer ![]() . Similarly, bet 4. implies
. Similarly, bet 4. implies ![]() and thus a contradiction.
and thus a contradiction.
![]()
There are several approaches to deal with uncertainty in a proper way, though. One way to deal with uncertainty is to use so-called capacities instead of probability measures ![]() .
.
In this post, however, we investigate so-called Imprecise Probabilities. The basic idea is to use a collection of probability measures (e.g. interval or set-valued probabilities), rather than a single (seemingly precise) distribution to model an uncertain event. Imprecise probabilities offer a framework for representing and reasoning about uncertainty in a more flexible and less seemingly precise manner than traditional probability theory.
We are going to focus on the theory put forward by Peter Walley [1]. However, this article is also based on [2] and [3]. Both are well-written and provide a good introduction and an overview on the topic of uncertainty.
Imprecise probabilities recognize that in many real-world situations, it’s difficult to assign precise numerical probabilities to events due to limited information or subjective uncertainty. Instead of a single precise probability value, imprecise probabilities use intervals, sets, or other structures to describe the range of possible probabilities.
We focus on the definition, basic properties and examples in the present Part I.
Part II is based on Part I and studies properties and structures of imprecise probabilities.
Overview
Let us assume that we are uncertain about the outcome of an event, that can be modeled using a set ![]() . The theory of imprecise probabilities is developed in terms of mathematical model
. The theory of imprecise probabilities is developed in terms of mathematical model ![]() , whereby
, whereby
 is a set of possible states of affairs of this event,
is a set of possible states of affairs of this event,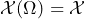 is a class of –i.e. the set of all– gambles on which
is a class of –i.e. the set of all– gambles on which- a real-valued set function
 , called lower prevision, is defined.
, called lower prevision, is defined.
The so-called conjugate real-valued set function ![]() , called upper prevision, can be derived via the relationship
, called upper prevision, can be derived via the relationship ![]() .
.
Hence, it is basically sufficient to focus just on lower or upper previsions.
![]() is the set of possible outcomes, short possibility space, of a well-defined event, experiment, observations, occurrences, or any conceivable facts about the real world. In classical probability theory
is the set of possible outcomes, short possibility space, of a well-defined event, experiment, observations, occurrences, or any conceivable facts about the real world. In classical probability theory ![]() is the sample space.
is the sample space.
A possibility space ![]() for the event is a finite or infinite set of elementary events
for the event is a finite or infinite set of elementary events ![]() , i.e., mutually exclusive outcomes
, i.e., mutually exclusive outcomes ![]() , that is exhaustive in the sense that other outcomes are deemed practically or pragmatically impossible. In classical probability theory, the possibility space
, that is exhaustive in the sense that other outcomes are deemed practically or pragmatically impossible. In classical probability theory, the possibility space ![]() is called sample space.
is called sample space.
A gamble ![]() is a bounded, real-valued function on
is a bounded, real-valued function on ![]() , where
, where ![]() can be interpreted as an uncertain reward or payoff whose value depends on the uncertain state
can be interpreted as an uncertain reward or payoff whose value depends on the uncertain state ![]() . In classical probability theory,
. In classical probability theory, ![]() is called a random variable. The set of all gambles is denoted by
is called a random variable. The set of all gambles is denoted by ![]() .
.
A gamble is desirable for us, if we accept ownership of it when offered to us. Either as a bet that we buy or as a bet that we sell. Whether one is willing to accept a gamble depends on one’s belief in the outcome ![]() .
.
We model uncertainty about the event’s outcome (i.e. about the probability distribution of the possibilities) using a set of all desirable gambles ![]() . That is, neither a single gamble
. That is, neither a single gamble ![]() nor its function values
nor its function values ![]() are uncertain. The uncertainty is reflected in a collection of different gambles instead of just considering one gamble.
are uncertain. The uncertainty is reflected in a collection of different gambles instead of just considering one gamble.
Desirability Axioms & Function Vector Spaces
We equip the set of all gambles ![]() with point-wise addition, point-wise scalar multiplication with real numbers
with point-wise addition, point-wise scalar multiplication with real numbers ![]() , and the supremum norm (topology). Then,
, and the supremum norm (topology). Then, ![]() forms a normed real function vector space
forms a normed real function vector space ![]() over
over ![]() , the bounded function (Banach) space to be precise.
, the bounded function (Banach) space to be precise.
Lower and upper previsions require commitments to act in certain rational ways, which is also reflected in the utility function of the decision-maker in the framework of imprecise probabilities.
As we know, a gamble is desirable for us, if we accept ownership of it when offered to us. We require the rationality criteria (D1) — (D4) as a logical consequence of the theory of upper and lower previsions.
Precise and Linear Subjective Utility Function
The key axiom (D1) and (D2) of the theory is that the utility for the outcome of a gamble is a linear function of the amount of the commodity that the individual gain from it. In other words, the personal utility function for the commodity is precise and linear. These assumptions are key since these requirements directly form a linear function vector space, in which we can model imprecise probabilities.
The theory of upper and lower previsions require commitments to act in certain rational ways. Let us first consider the following two out of four axioms.
(D1) If ![]() is desirable and
is desirable and ![]() then
then ![]() is desirable, i.e.,
is desirable, i.e., ![]()
(D2) If ![]() and
and ![]() are each desirable then
are each desirable then ![]() is desirable, i.e.,
is desirable, i.e., ![]()
Recall that the uncertainty about the event’s outcome is reflected in a set of desirable gambles ![]() . By this, we split the set of all gambles
. By this, we split the set of all gambles ![]() into desirable
into desirable ![]() and not desirable gambles
and not desirable gambles ![]() . (D1) and (D2), in effect, require that the scale in which rewards
. (D1) and (D2), in effect, require that the scale in which rewards ![]() are measured behaves like a linear utility scale and therefore inherits the vector space structure from
are measured behaves like a linear utility scale and therefore inherits the vector space structure from ![]() . That is, the criteria of a linear subspace serve as axioms.
. That is, the criteria of a linear subspace serve as axioms.
(D1) states that if you scale a desirable gamble with a positive real figure, it should still be desirable. So if you are offered a desirable gamble you should also accept each positive multiple of it.
Assume, we have two desirable gambles ![]() , then
, then ![]() is also accepted and thus considered desirable, i.e.,
is also accepted and thus considered desirable, i.e., ![]() as stated in (D2).
as stated in (D2).
Acccording to (D1) and (D2), a gamble’s desirability should be independent of the stake and the combination of two desirable gambles should also be desirable. In the context of imprecise probabilities, desirability is closely related to the idea of utility or value.
Avoiding Sure Loss and Accepting Sure Gain
The following questions (refer to [3]) are pivotal to the concept of desirability:
- Do we need to specify desirability for each gamble individually?
- Do we have to consider some specific sets of gambles to be desirable or not desirable?
- Can we argue that if some gambles are desirable, then other should be as well, i.e., can we automatically extend a partial specification?
The answer to the last question 3. is obvious given the result from last section about the vector space structure of ![]() . The linear hull of each
. The linear hull of each ![]() also has to be desirable. The answer to 1. is therefore ‘no’.
also has to be desirable. The answer to 1. is therefore ‘no’.
Are there compelling reasons to insist that some gambles should be desirable or not desirable, independent of the information available to us about the event’s outcome?
And indeed there are:
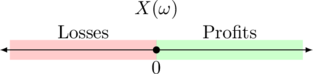
Any gamble that gives a positive payoff or reward without ever giving a negative one needs to be considered desirable in this setting. In addition, any gamble that gives a negative payoff or reward without ever giving a positive one needs to be considered not desirable.
These two criteria can be formalized as follows:
(P1) Accepting partial loss
If ![]() then
then ![]() or
or ![]()
(P2) Accepting partial gain
If ![]() then
then ![]() or
or ![]()
Note that ![]() means that for all
means that for all ![]() the function value
the function value ![]() is always greater than zero. Thereby,
is always greater than zero. Thereby, ![]() can also be interpreted as the zero gamble, where you get
can also be interpreted as the zero gamble, where you get ![]() for every possibility
for every possibility ![]() .
.
That is, you are certain about the gains and losses and thus certain about the final payoff as sketched in the following graph. No matter which ![]() is going to realize, we already know that the outcome will be positive and thus the function value lies in quadrant I. A toy illustration is shown in Fig. 2 below.
is going to realize, we already know that the outcome will be positive and thus the function value lies in quadrant I. A toy illustration is shown in Fig. 2 below.
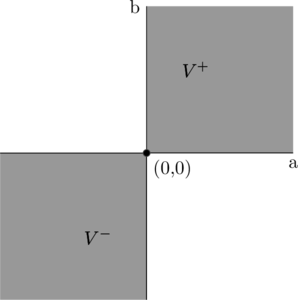
Fig. 2: Sketch of a function vector space with a two-element possibility space ![]() . The highlighted quadrants I and III reflect the possible function values
. The highlighted quadrants I and III reflect the possible function values ![]() and
and ![]()
We see that the so-called positive orthant ![]() and negative orthant
and negative orthant ![]() must, respectively, be included in and excluded from the set
must, respectively, be included in and excluded from the set ![]() .
.
In addition, ![]() and
and ![]() is not a vector (sub-)space since the additive inverse is not an element of
is not a vector (sub-)space since the additive inverse is not an element of ![]() and
and ![]() , respectively.
, respectively.
Let us now slightly relax the requirements made in (P1) and (P2) and assume you are offered a gamble, where you are either guaranteed to
- experience a loss regardless of the decision you made, i.e.,
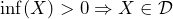 or
or 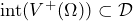
- experience a gain regardless of the decision you made, i.e.,
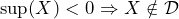 or
or 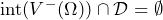 .
.
Note that ![]() is the interior of a set.
is the interior of a set.
This effectively means that there is no uncertainty about the fact that the decision will result in either a loss or a gain. The theory of lower and upper previsions requires that such gambles where you are sure about a loss are not considered to be desirable. Likewise, gambles where you are sure about a gain are considered to be desirable. Let us formalize these rationality criteria according to the theory of lower and upper previsions in the following axioms.
(D3) Avoiding sure loss
If ![]() then
then ![]() is not desirable.
is not desirable.
(D4) Accepting sure gain
If ![]() then
then ![]() is desirable.
is desirable.
Lower and Upper Previsions
The theory of imprecise probabilities consider gambles, whose possible outcomes are gains or losses of a single commodity.
Lower and upper previsions generalize probabilities and expectations we usually encounter in the classical probability theory, though this theory falls squarely within the subjective approach of probability.
Subjective means in this context behavioral, that is, a subject’s probability (i.e. belief) for an event reflects his willingness to take certain actions whose outcome depends on its occurrence, such as accepting bets on or bets against the event at certain betting rates.
The outcome of a gamble ![]() is uncertain and depends on the events
is uncertain and depends on the events ![]() of interest as well as on the utility function of the individual decision-maker. Recall that a gamble
of interest as well as on the utility function of the individual decision-maker. Recall that a gamble ![]() is a bounded real-valued map on the possibility space. It represents an uncertain reward, whose value is
is a bounded real-valued map on the possibility space. It represents an uncertain reward, whose value is ![]() if the outcome of the experiment is
if the outcome of the experiment is ![]() . This reward is expressed in units of some linear utility scale as outlined in the section before.
. This reward is expressed in units of some linear utility scale as outlined in the section before.
The theory of lower previsions considers two types of transactions involving a gamble ![]() :
:
- Accepting to buy
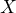 for a price
for a price 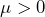 , which comes down to accepting the gamble
, which comes down to accepting the gamble 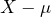
- Accepting to sell
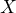 for a price
for a price 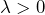 , which comes down to accepting the gamble
, which comes down to accepting the gamble 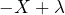
Note that ![]() is the buying or ask price that we receive as a seller while
is the buying or ask price that we receive as a seller while ![]() is the selling or bid price we need to pay as a buyer. Inflows and outflows relative to a certain party are represented by positive and negative signs, respectively.
is the selling or bid price we need to pay as a buyer. Inflows and outflows relative to a certain party are represented by positive and negative signs, respectively.
Let us now assume that a bet ![]() has been accepted by both parties of the deal, i.e. by the seller and the buyer. This implies that a price
has been accepted by both parties of the deal, i.e. by the seller and the buyer. This implies that a price ![]() is acceptable for both, i.e., the corresponding bid-ask spread is zero. Figure 3 illustrates the payoffs for both parties in this case. Note that
is acceptable for both, i.e., the corresponding bid-ask spread is zero. Figure 3 illustrates the payoffs for both parties in this case. Note that ![]() can be positive and negative.
can be positive and negative.

Fig. 3: Exchange of cash flows to the buyer and seller. The payoff of the gamble ![]() depends on the event
depends on the event ![]() that realizes and might be positive or negative for the buyer. That is, the outcome of
that realizes and might be positive or negative for the buyer. That is, the outcome of ![]() is uncertain
is uncertain
We denote ![]() for the infimum (greatest lower bound) and
for the infimum (greatest lower bound) and ![]() for the supremum (least upper bound). Both
for the supremum (least upper bound). Both ![]() as well as
as well as ![]() are finite since a gamble is bounded by definition. We write
are finite since a gamble is bounded by definition. We write ![]() if
if ![]() for all
for all ![]() .
.
A subject’s lower prevision ![]() for a gamble
for a gamble ![]() represents his supremum acceptable buying or ask price for
represents his supremum acceptable buying or ask price for ![]() , which is the highest price
, which is the highest price ![]() such that the subject accepts to buy
such that the subject accepts to buy ![]() for all prices
for all prices ![]() . In other words
. In other words
(1) ![]()
where ![]() is the set of gambles that our subject finds desirable. (1) implies that the subject is willing to pay
is the set of gambles that our subject finds desirable. (1) implies that the subject is willing to pay ![]() for the uncertain reward
for the uncertain reward ![]() , or in other words, that the transaction
, or in other words, that the transaction ![]() is desirable for the subject for every
is desirable for the subject for every ![]() . Nothing is said about whether the subject would actually buy the gamble
. Nothing is said about whether the subject would actually buy the gamble ![]() for the price
for the price ![]() given the definition of the supremum.
given the definition of the supremum.
We can also consider our subject’s upper prevision, or infimum acceptable selling or bid price, for the gamble ![]() , which we denote by
, which we denote by ![]() . It is the lowest price
. It is the lowest price ![]() such that the subject accepts to sell
such that the subject accepts to sell ![]() for all prices
for all prices ![]() . In other words
. In other words
(2) ![]()
(2) implies that the subject is willing to sell the gamble ![]() for
for ![]() . That is, the transaction
. That is, the transaction ![]() is desirable for the subject for every
is desirable for the subject for every ![]() . Again, nothing is said about the price
. Again, nothing is said about the price ![]() itself.
itself.

Fig. 5: Illustration of upper and lower prevision of a buyer and a seller
The following Fig. 6 illustrates the general interrelation between the lower and upper prevision focused on the payoff function compared to the situation as shown in Fig. 5.

Fig. 6: Interrelation between the lower and upper prevision in the general case, i.e. when the lower prevision does not necessarily meet the upper prevision.
Note that a fair (market) price exists if lower and upper prevision meet. In this case no ‘undecided’ interval exists.
Let us apply the theory in the next example.
Example 4.1 (Urn, modified version taken from [1]):
Suppose a ball is drawn from an urn with red, white and black balls. We are offered a reward depending on the color of the ball:
- We get €10 if red ball is drawn,
- we get €5 if a white ball is drawn, and
- we get €0 if a black ball is drawn.
The corresponding gamble ![]() is based on the possibility space
is based on the possibility space ![]() , where
, where ![]() ,
, ![]() and
and ![]() stands for ‘black’, ‘red’ and ‘white’, respectively. That is,
stands for ‘black’, ‘red’ and ‘white’, respectively. That is, ![]() is defined by
is defined by
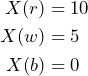
The bet ![]() is desirable since all payoffs are not negative. In addition, we might be willing to pay some fixed amount of money, say
is desirable since all payoffs are not negative. In addition, we might be willing to pay some fixed amount of money, say ![]() €, in order to buy the gamble and thus to receive the uncertain reward. We are going to suppress the € symbol in the rest of this example.
€, in order to buy the gamble and thus to receive the uncertain reward. We are going to suppress the € symbol in the rest of this example.
The increase in wealth for the buyer would be ![]() . That is,
. That is, ![]() if a red ball is drawn,
if a red ball is drawn, ![]() if a white ball is drawn, and
if a white ball is drawn, and ![]() if a black ball is drawn.
if a black ball is drawn.
The supremum amount of money ![]() , we are willing to pay to buy the gamble, will be our lower prevision
, we are willing to pay to buy the gamble, will be our lower prevision ![]() for the gamble
for the gamble ![]() .
.
If, for instance, we are absolutely certain that there is no black ball in the urn, we should be disposed to pay up to ![]() since this is the least we will get given the subject’s belief. In other words, the wealth will not be decreased no matter what event –i.e. a red or a white ball is drawn– will arise. Hence, the subject will assume some sort of worst case given its belief.
since this is the least we will get given the subject’s belief. In other words, the wealth will not be decreased no matter what event –i.e. a red or a white ball is drawn– will arise. Hence, the subject will assume some sort of worst case given its belief.
If, for instance, the subject is sure that only red balls are in the urn, then we the buyer should pay less than 10 since +10 is the worst payoff the buyer can have given his belief.
On the other hand, we could also consider selling the gamble ![]() for a fixed price
for a fixed price ![]() . Our increase in wealth will then be
. Our increase in wealth will then be ![]() if the red ball is drawn,
if the red ball is drawn, ![]() if the white ball is drawn, and
if the white ball is drawn, and ![]() if the black ball is drawn. The infimum amount of money
if the black ball is drawn. The infimum amount of money ![]() , that we require in order to sell
, that we require in order to sell ![]() , will be his upper prevision
, will be his upper prevision ![]() .
.
If, for instance, the seller is absolutely certain that there are only red and white balls in the urn, he should accept to sell for any price ![]() . Apparently,
. Apparently, ![]() is the worst payoff the seller can have in the gamble under this condition.
is the worst payoff the seller can have in the gamble under this condition.
![]()
The last example demonstrated that the price, that a rational buyer is willing to pay and a rational seller is willing to sell for this gamble, respectively, depends on the presumed distribution of the white, red and black balls in the urn.
If we generalize that observation, we can see that the prize of a gamble directly depends on probabilities assigned to the possibilities ![]() .
.
If ![]() on
on ![]() with possibility set
with possibility set ![]() is a lower prevision, the conjugate upper prevision
is a lower prevision, the conjugate upper prevision ![]() is defined on the domain
is defined on the domain ![]() by
by ![]() . A benefit under a lower is going to be a loss under an upper prevision. Note that
. A benefit under a lower is going to be a loss under an upper prevision. Note that ![]() may be defined on a different domain from
may be defined on a different domain from ![]() .
.
In the theory of lower and upper previsions, we are not paying attention to the subject’s entire set of desirable gambles ![]() but rather try to model our subject’s belief by looking directly at this lower and upper previsions for a number of gambles.
but rather try to model our subject’s belief by looking directly at this lower and upper previsions for a number of gambles.
Recall that we model uncertainty about an event’s outcome (i.e. about the probability distribution of the possibilities) using a set of all desirable gambles of a subject. Suppose our subject assesses lower previsions ![]() for all gambles
for all gambles ![]() on some subset
on some subset ![]() . This defines a real functional
. This defines a real functional ![]() , which is the lower prevision with domain
, which is the lower prevision with domain ![]() . There is an analog definition for the upper prevision with domain
. There is an analog definition for the upper prevision with domain ![]() .
.
Since selling a gamble ![]() for a price
for a price ![]() is the same thing as buying the gamble
is the same thing as buying the gamble ![]() for the price
for the price ![]() , buyer and seller need to be disposed to accept these transactions under the same conditions. Hence, the seller’s infimum acceptable selling price need to agree with the buyer’s supremum acceptable buying price for
, buyer and seller need to be disposed to accept these transactions under the same conditions. Hence, the seller’s infimum acceptable selling price need to agree with the buyer’s supremum acceptable buying price for ![]() . Again, in this case the bid-ask-spread is zero, i.e.
. Again, in this case the bid-ask-spread is zero, i.e. ![]() as illustrated in Fig. 4:
as illustrated in Fig. 4:
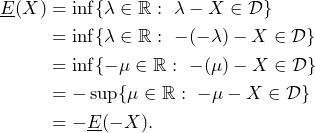
As a consequence, given the lower prevision ![]() on a set of gambles
on a set of gambles ![]() , we can define the so-called conjugate upper prevision
, we can define the so-called conjugate upper prevision ![]() on
on ![]() , by
, by ![]() , and vice versa. Taking this into account, as we can freely go from one concept to the other, it suffices to discuss only one of them.
, and vice versa. Taking this into account, as we can freely go from one concept to the other, it suffices to discuss only one of them.
Without loss of generality, we are going to focus on lower previsions or to put it differently on the buying side.
Coherent Sets of Desirable Gambles
The axioms (D1) – (D4) are fundamental for the theory of imprecise probabilities. The first two axioms (D1) and (D2) basically require that the set ![]() , that contains all desirable gambles, is a (function) vector space.
, that contains all desirable gambles, is a (function) vector space.
What about (D3) and (D4)?
Let us consider axiom (D3) closer. Let ![]() be the buying price for the gamble
be the buying price for the gamble ![]() . If
. If ![]() is negative no matter what outcome
is negative no matter what outcome ![]() is going to be, then
is going to be, then ![]() needs to be a non-desirable gamble.
needs to be a non-desirable gamble.
Hence, from a buyer perspective a desirable gamble needs to fulfill the condition
(3) ![]()
If ![]() for all
for all ![]() , then it’s going to be a sure overall loss for the buyer. This needs to be avoided according to axiom (D3), such that the difference of both need to be positive for some
, then it’s going to be a sure overall loss for the buyer. This needs to be avoided according to axiom (D3), such that the difference of both need to be positive for some ![]() .
.
The in-equation (3) requires that the overall payoff ![]() is at least of positive utility for some
is at least of positive utility for some ![]() . Hence, it is sufficient in (3) to check the best case(s), i.e. to take the supremum over
. Hence, it is sufficient in (3) to check the best case(s), i.e. to take the supremum over ![]() .
.
If we apply the additivity axiom (D2) to a finite set of desirable gambles ![]() with
with ![]() and
and ![]() , it follows that
, it follows that
(4) ![Rendered by QuickLaTeX.com \begin{align*} \sup_{\omega\in \Omega}\ \{ \sum_{i=1}^{n} \left[ X(\omega) - \underline{E}( X(\omega) ) \right] \} \ \geq 0. \end{align*}](https://www.deep-mind.org/wp-content/ql-cache/quicklatex.com-5dd92122830180c2dfa5d148be418150_l3.png)
To motivate condition (4), assume that it is not satisfied. Then there are ![]() ,
, ![]() in
in ![]() , and
, and ![]() such that
such that
![Rendered by QuickLaTeX.com \begin{align*} \sum_{i=1}^{n}{ \left[ X_i - \underline{E}(X_i) +\epsilon \right] } \leq -\epsilon, \end{align*}](https://www.deep-mind.org/wp-content/ql-cache/quicklatex.com-ca61bed43515b032d0121df133016818_l3.png)
meaning that the sum of the desirable gambles ![]() results in a loss of at least
results in a loss of at least ![]() , no matter the outcome of the event
, no matter the outcome of the event ![]() . Since the sum needs to be desirable by (D3), this violates (D1). Contradiction.
. Since the sum needs to be desirable by (D3), this violates (D1). Contradiction.
![]()
Let us try to illustrate that in an example.
Example 5.1 (Urn continued)
A subject is faced with the bet ![]() as outlined in Example 4.1:
as outlined in Example 4.1:
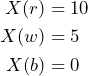
The subject is absolutely certain that there is no black ball in the urn, such that he is disposed to pay up to ![]() since this is the least he will get given his belief. Therefore, he is avoiding a sure loss for the gamble
since this is the least he will get given his belief. Therefore, he is avoiding a sure loss for the gamble ![]() based on his belief.
based on his belief.
Another gamble ![]() , defined by
, defined by
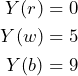
, is also offered to this subject. Let us assume the subject is willing to pay 6 for the bet ![]() , then the overall payoff for both bets is determined by
, then the overall payoff for both bets is determined by
Realize that the subject needs to invest ![]() to buy both bets
to buy both bets ![]() and
and ![]() . This means that the infimum acceptable buying price
. This means that the infimum acceptable buying price ![]() is always higher than in any outcome
is always higher than in any outcome ![]() . It is therefore certain to loose no matter what event is going to materialize, i.e. a sure loss.
. It is therefore certain to loose no matter what event is going to materialize, i.e. a sure loss.
Hence, given axiom (D3) the subject must not accept a buying price of 6 for the bet ![]() . In addition, the subject is sure that there is no black ball in the urn. Given its belief, the buyer gets its lowest reward of
. In addition, the subject is sure that there is no black ball in the urn. Given its belief, the buyer gets its lowest reward of ![]() under
under ![]() if a red ball is drawn.
if a red ball is drawn.
Let us assume that our subject is willing to pay 4 for the bet ![]() after some reflection.
after some reflection.
In this case the overall payoff including the buying price ![]() is as follows:
is as follows:
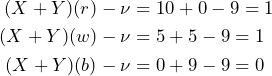
Paying 4 for ![]() will avoids a sure loss. Let us wrap it up considering the subjects point of view. The supremum acceptable buying price
will avoids a sure loss. Let us wrap it up considering the subjects point of view. The supremum acceptable buying price ![]() equals 5 and the supremum acceptable buying price
equals 5 and the supremum acceptable buying price ![]() is 4.
is 4.
![]()
There is a stronger rationality condition called coherence.
It requires that our subject’s supremum acceptable buying price for a gamble ![]() cannot be raised by considering a positive linear combination of a finite number
cannot be raised by considering a positive linear combination of a finite number ![]() of other acceptable gambles. That is,
of other acceptable gambles. That is,
(5) ![Rendered by QuickLaTeX.com \begin{align*} \sup_{\omega\in \Omega} \{ & \sum_{i=1}^{n}{ \left[ X_i - \underline{E}(X_i) +\epsilon \right] } \\ &-m[X_0-\underline{E}(X_0) +\epsilon] \} \geq 0, \end{align*}](https://www.deep-mind.org/wp-content/ql-cache/quicklatex.com-dad30532e895302d9acf8300bfbda85e_l3.png)
for all natural ![]() and all
and all ![]() . A lower prevision satisfying the condition (5) will particular avoid sure loss — just consider the case
. A lower prevision satisfying the condition (5) will particular avoid sure loss — just consider the case ![]() along with condition (4). In addition, note that the gambles in (5) obviously depend on the realization
along with condition (4). In addition, note that the gambles in (5) obviously depend on the realization ![]() .
.
Let us show that coherence is consistent with the desirability axioms. Suppose that equation (5) does not hold for some non-negative integers ![]() and some
and some ![]() in
in ![]() . If
. If ![]() , this means that
, this means that ![]() incurs a sure loss, which we have already argued is an inconsistency. Assume therefore that
incurs a sure loss, which we have already argued is an inconsistency. Assume therefore that ![]() , then there is a
, then there is a ![]() such that
such that
![Rendered by QuickLaTeX.com \begin{align*} \sum_{i=1}^{n}&{ \left[ X_i - \underline{E}(X_i) +\epsilon \right] } \ \leq \\ & m[X_0-(\underline{E}(X_0)+\epsilon)]. \end{align*}](https://www.deep-mind.org/wp-content/ql-cache/quicklatex.com-37058cb057ce55c8163ee0a866e92e98_l3.png)
The left-hand side is a sum of desirable transactions, and should therefore be desirable, by axiom (D2). The dominating right-hand side should be desirable as well since it offers an even higher overall payoff. This, however, means that our subject should accept to buy the gamble ![]() for the price
for the price ![]() , which is strictly higher than the supremum buying price he has specified for it. This is again an inconsistency that, is ruled out by the coherence condition.
, which is strictly higher than the supremum buying price he has specified for it. This is again an inconsistency that, is ruled out by the coherence condition.
Further Examples
In the last five chapters, we have studied the definition and basic properties of imprecise probabilities and used urn examples to illustrate these. In this chapter, we are going to look at other example types including those examples that are also used in classical probability theory such as rolling dices and flipping coins.
Most people and most examples in classical probability theory assume that all outcomes of flipping a coin are equally likely. The € coin has been accused of not being fair, i.e., that heads is more likely than tails landing face upwards.
Example 6.1 (Flipping a €-Coin)
A subject’s belief is that a German €-coin lands more often on heads than on tails, i.e. that the probability of landing head upwards is in ![]() . Correspondingly, the likelihood of landing tails upwards lies between
. Correspondingly, the likelihood of landing tails upwards lies between ![]() and
and ![]() .
.
What supremum buying price is the subject willing to pay therefore for carrying out 1,000 of the following bet ![]() ?
?
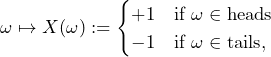
If the coin is fair, the expected value of a series of 1,000 of these bets is zero. Given the subject’s belief, the supremum buying price is €![]() € 1,000.
€ 1,000.
The subject would not accept to sell this bet since according to his belief, he can only make a loss between €20 and €50. Otherwise, this would contradict axiom (D3) of avoiding a sure loss.
![]()
The possibility space ![]() of a six-sided dice is just as in the classical case with
of a six-sided dice is just as in the classical case with ![]() . When it comes to rolling a six-sided dice, most of us assume that each number from 1 to 6 has a chance of
. When it comes to rolling a six-sided dice, most of us assume that each number from 1 to 6 has a chance of ![]() of landing face up. But this holds only true if the dice is a perfectly balanced cube. So what if our trusty dice is not as precise as we think?
of landing face up. But this holds only true if the dice is a perfectly balanced cube. So what if our trusty dice is not as precise as we think?
Example 6.2 (Rolling Dice)
A subject’s belief is that a certain die might not be perfectly balanced, i.e., that even numbers show up more often than odd numbers. This belief might be based on some empirical observations that the odd numbers are less likely to show face upwards. Hence, it is more desirable for the subject to bet on the occurrence of even numbers.
That is, the subject beliefs that the probability of the event ![]() lies somewhere between
lies somewhere between ![]() and
and ![]() . Since the rolling dices are independent events, the corresponding probability of
. Since the rolling dices are independent events, the corresponding probability of ![]() is believed to lie somewhere between
is believed to lie somewhere between ![]() and
and ![]() .
.
What supremum buying price is the subject willing to pay therefore for carrying out 1,000 of the following bet ![]() ?
?
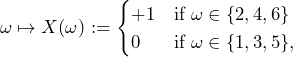
If the subject thinks that the actual probability of the event ![]() is in
is in ![]() , the expected payoff of 1,000 bets
, the expected payoff of 1,000 bets ![]() lies between € 500 and € 520. Provided that his belief turns out to be true, the worst expected payoff would lie above €500. This in return, is the supremum buying price
lies between € 500 and € 520. Provided that his belief turns out to be true, the worst expected payoff would lie above €500. This in return, is the supremum buying price ![]() of the subject for this series of bets. That is, the subject should not pay more than € 500 to buy this series of bets.
of the subject for this series of bets. That is, the subject should not pay more than € 500 to buy this series of bets.
Applying the concept of imprecise probabilities, we can reflect the subject’s uncertainty by the intervals ![]() for the likelihood of landing heads upwards.
for the likelihood of landing heads upwards.
The corresponding upper prevision ![]() of the series of bets is
of the series of bets is ![]() . This represents the infimum selling price of the series of 1,000 bets
. This represents the infimum selling price of the series of 1,000 bets ![]() . Given our belief the worst scenario that can happen is that we need to pay € 520, which in return means that this is the infimum selling price of that series of bets.
. Given our belief the worst scenario that can happen is that we need to pay € 520, which in return means that this is the infimum selling price of that series of bets.
![]()
Our last example delves into the realm of a market maker [6], a trader who provides quotes to other market participants at which he stands ready to buy and sell a given asset. A market maker
- makes money out of buying low and selling high (bid-ask spread) while facing the risk that the price moves adversely without him being able to unwind his position rapidly enough;
- must be able to adapt quickly to changing market conditions;
- is exposed to the risk that the price moves against them, in particular, in a volatile market.
A market maker faces a constant trade-off between several competing objectives. A typical trade-off is, for instance, to either choose a high-margin and low-volume versus low-margin and high-volume market. There are, however, many other connected objectives such as being compliant, having a low inventory of the traded assets and to keep an overall low level of risk.
In a broad sense, a market maker is therefore a liquidity supplier, who faces a hard optimization problem that has been addressed in a long list of academic papers. Most mathematical models assume an arithmetic Brownian motion of the asset set in a classical probability space.
Instead of using classical probability spaces and stochastic processes such as a Brownian motion with exact probabilities to model bid and ask quotes, we can employ the theory of imprecise probabilities. There are several ways to do so and it ultimately depends on the subject’s belief and objectives.
Example 6.3 (Quotes Allianz SE stock)
The market maker of Allianz SE stock is uncertain about the price development. The last available price is €240 from yesterday. Because of some recent events, he expects that the next market price of the stock should lie somewhere in ![]() .
.
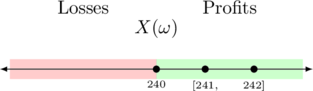
This situation can be modeled using the discrete possibility space ![]() considering the ticks, i.e., the smallest unit by which the price of an asset can change. The market maker has an inventory of the Allianz SE stock bought at an price of €
considering the ticks, i.e., the smallest unit by which the price of an asset can change. The market maker has an inventory of the Allianz SE stock bought at an price of €![]() . The gamble can therefore be modeled by the function
. The gamble can therefore be modeled by the function
![]()
The market maker will only gain, if the stock price is greater than € 240. His lower and upper prevision is 241 and 242, respectively.
The bid price is the highest price a buyer / bidder is willing to pay. Correspondingly, the ask price is the lowest price a seller is willing to accept. These definitions suit the definition of a lower and upper prevision obviously.
However, it would also be possible to employ the theory of imprecise probabilities on the bid and ask price separately. That is, to model the uncertainty around the bid price, for instance, separately.
![]()
Literature
The Standford Encyclopedia of Philosophy contains a good introduction to the theory of Imprecise Probabilities.
[1]
[2]
[3]
[4]
[5] Conditional Probabilities and the Bayes Theorem by Alexander von Felbert
[6] Mathematical modeling for market making and related problems of financial liquidity: a song of assets and traders by Philippe Bergault


